大家好！从今天开始，我们将用六节课的时间详细讲解二年级数学二次根(下册)，同时会有视频课。欢迎学习。

二次根式的定义

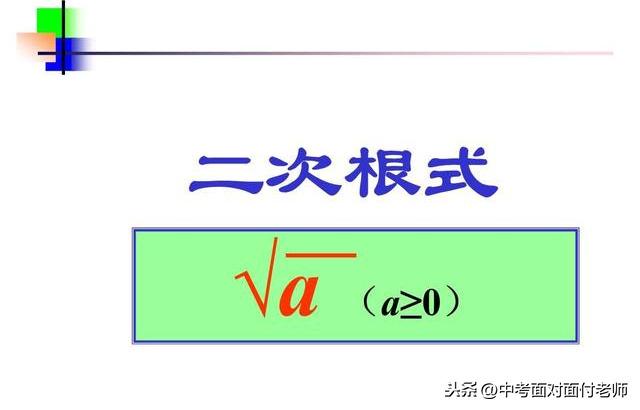
什么是平方根？ √a(a≥0)这样的公式叫做二次根式。其中a称为根号，“√”称为根号或二次根号。如√3，√ x+1，3√2等。

1.二次根的两个元素:

①必须有一个次根号“√”；

②处方数非负。

2.二次方根的有意义条件:

根号必须是非负的，即根号以下的代数表达式a≥0。

例如，当x是实数时，下列表达式在实数范围内有意义？(1)√x+3；(2)√x -1 .

解:(1)根据二次方根公式的有意义条件，平方根个数必须非负，才能得到x+3≥0，解为x ≥- 3；

(2)根据二次根公式的有意义条件，要取的根数必须是非负的，这样才能得到x-1 ≥ 0，x≥1或x≤-1才能求解。

3.特别提醒:对于二次方根的理解，要注意三点。

①从形式上看，必须包含次根号“√”；

②根号A不仅是一个数(非负)，而且是一个具有非负值的代数表达式；

③平方根√a(a≥0)表示非负a的算术平方根。

平方根公式必须满足的条件

最简单的二次方根是什么？ 满足以下两个条件的根是最简单的二次根:①根号的因子是整数，因子是代数表达式；(2)平方根的个数不包含平方根的整数或代数表达式。

比如:(1) √ x (x ≥ 0)，因为x是x，所以√ x不是最简单的二次根式。

(2)√4x中的因子4可以开根号，结果是2，所以√4x不是最简单的二次方根。简化结果√ 4x = 2 √ x。

二次根式

同类的二次方根是什么？ 在之前的七年级数学中，我们学习了“相似项”，所以同学们可以结合“相似项”的定义来理解相似二次根。比如2x和3x是相似项，即字母部分相同的单项式是相似项。所以，我们联系一下，看看类似的二次方根是什么。

定义:将几个二次根化简为最简单的二次根后，如果根的个数相同，则称这几个二次根为相同的二次根。比如√x和2√x是相似的二次方根，√3和2√3是相似的二次方根。

温馨提示:

从上面提到的最简单的二次方根和相似的二次方根不难看出，这两者前后联系紧密，所以大家在学习的时候一定要把每一个知识点都弄懂，这样才不会出现“知识断层”，否则前后不衔接，自然数学学的就差了。

特别提醒:对于相似二次根的判断，大多数情况下不会直接给出最简单的二次根供你判断是否为相似二次根，所以要求学生先简化，再根据要开的根的个数是否相同来判断哪些是相似二次根。