在今年的圆周率日(3月14日)，人类打破了一项新的世界纪录——圆周率的小数位数被计数到史无前例的31.4万亿。那么，不断计算圆周率有什么实际意义呢？小数几万亿的圆周率还不够吗？

3000多年前人们就开始使用圆周率了。古人发现，无论多大的圆，其周长与直径之比总是一个固定的常数，这个常数就是圆周率。但是圆周率一直没有精确计算出来，人们想尽办法提高圆周率的计算精度。

最早计算圆周率的严谨方法是切圆法，古希腊和中国的数学家都使用这种方法。我国数学家祖冲之用这种方法将圆周率精确到小数点后第六位，这一精度800年来一直为世界之最。

从16世纪开始，数学家们开始使用更高效的无穷级数来计算圆周率。圆周率可以表示为无穷级数的和。一个有代表性的例子是莱布尼茨圆周率公式:

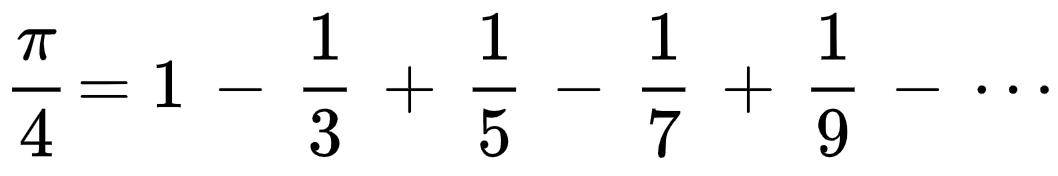
虽然计算圆周率的效率提高了很多，但是这个常数的小数位数好像还没算完。1761年，数学家终于证明了圆周率的小数位数是不可数的，因为它是一个无理数，有无穷多个无循环的小数位数。

拉马努金发现圆周率的计算公式

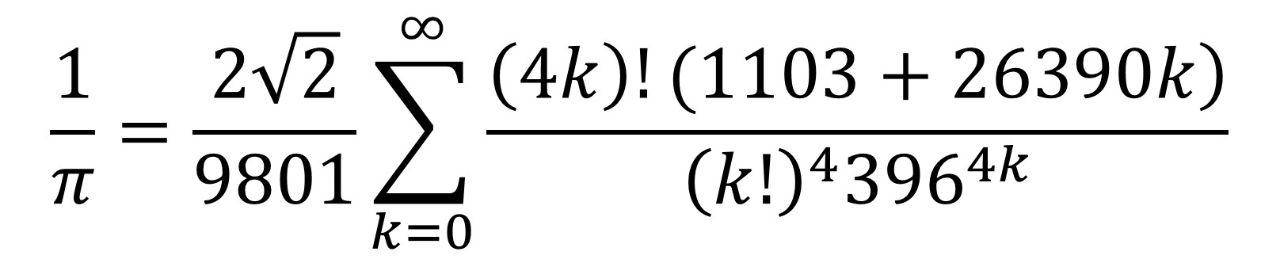
从此，人们对圆周率的计算不再是统计所有的小数位，而是不断完善小数位。除了圆周率的Ra*nukin公式收敛很快，还有计算速度更快的迭代算法。有了超级计算机，人类现在可以把小数位数到31.4万亿。

虽然我们计算了圆周率的很多小数位，但实际上用的位数很少。生活中，圆周率有两位小数就够了。即使在精度非常高的航空航天领域，也不需要小数点后20位的圆周率。

在理论物理中计算一些与pi有关的常数或参数时，需要非常高的精度，但只需要小数点后32位的pi。如果用小数点后40位的圆周率来计算半径为465亿光年的哈勃体积，得到的结果偏差没有一个氢原子大。

那么，既然知道圆周率是取之不尽的，为什么人类还要无休止地继续计算下去呢？这有什么现实意义？

人类计算圆周率的历史由来已久。计算机发明后不久就被用来计算圆周率。这种做法已经被用来测试超级计算机的性能。另外，圆周率的计算还有一个很简单的目的，就是不断打破世界纪录，拓展人类未知的领域。